The Platonic Representation Hypothesis
Motivated by the Platonic Representation Hypothesis—which suggests that diverse foundation models converge toward shared representations of reality—we explore whether synthetic data optimized for one architecture can train another.
We demonstrate that a single synthetic image per class is sufficient to train linear probes that not only achieve competitive performance across a diverse array of vision backbones (CLIP, DINO-v2, EVA-02) but consistently outperform baselines constructed from real images.
Method: Linear Gradient Matching
Our approach departs from traditional distillation which targets full network training. Instead, we target the regime of linear probing—training lightweight classifiers atop frozen, pre-trained feature extractors.
The core insight relies on two principles:
- For a linear probe, matching the gradient of the loss with respect to the weights is sufficient to align training trajectories.
- By minimizing the angular distance between gradients induced by real and synthetic data, we force synthetic images to encode features that point the optimization in the correct direction.
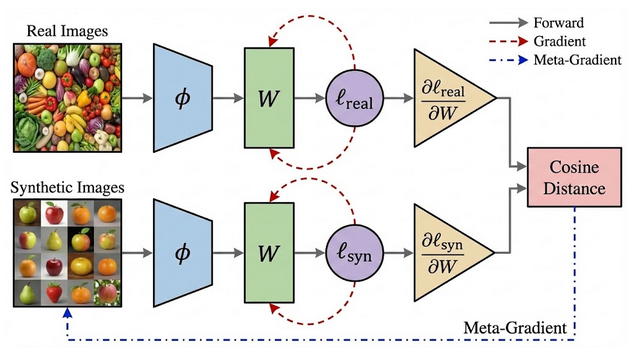
Figure 2: Linear Gradient Matching. We optimize synthetic pixels such that they induce the same gradient updates on a linear classifier as a batch of real data.
Why Synthetic Beats Real
A surprising finding in our research is that synthetic data often outperforms representative real data (such as class centroids). Why?
We hypothesize that gradient matching drives synthetic prototypes to the "boundary" of the class distribution to maximize discriminative power. As visualized below in the PCA projection:
- Real images (dots) cluster around the mean.
- Distilled images (stars) consistently locate themselves at the periphery, effectively acting as support vectors.
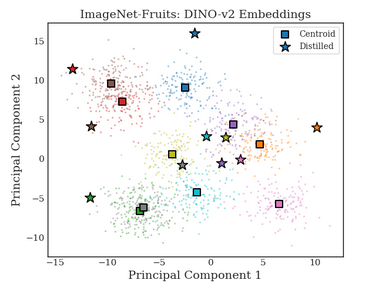
Figure 3: PCA Visualization. Real images (dots) cluster around the mean, while our distilled images (stars) push to the decision boundaries.
Diagnosing Model Biases
Beyond efficiency, these distilled datasets serve as potent diagnostic tools. They allow us to "see" what a model prioritizes. In our experiments with the "Spawrious" dataset (containing correlations like dogs on specific backgrounds), we found:
- DINO-v2: The distilled image retains the object (dog), showing robustness to background noise.
- MoCo-v3: The distilled image focuses almost entirely on the background. This explains why MoCo fails on the test set—it was looking at the wrong features.

Figure 4: Visualizing Spurious Correlations. The synthetic images expose the underlying biases of the models.
Conclusion
Linear Gradient Matching adapts dataset distillation to the pre-training era. By treating alignment as a quantifiable property of the gradient space, we have shown that it is possible to compress massive datasets into compact, transferable representations that not only train models efficiently but also illuminate the internal physics of their representations.
